Определения. Пусть требуется решить задачу (2): f(x) -->min,  хОRⁿ (2) В двумерном пространтсве R² решению такой задачи можно дать геометрическую иллюстрацию. Пусть точка х =(х₁,х₂) лежит на плоскости Ох₁х₂. Введем третью координату х₃ так, чтобы ось координат Ох₃ была перпендикулярна плоскости Ох₁х₂ (рис.1). Уравнению х₃ = f(х₁,х₂) соответствует поверхность в трехмерном пространстве.
Если функция f(х) достигает локального минимума в точке х*ОR², то поверхность в некоторой окрестности точки х*  имеет форму чаши (рис.1).

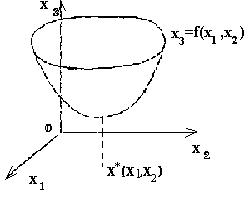
Рис.1

Напомним, что линиями уровня функции f(х₁,х₂) называют семейство линий плоскости R², на которых функция принимает постоянное значение. Неявным уравнением линии уровня является уравнение f(x₁,x₂)=C. Если функция f(x) имеет в R² единственную точку локального минимума  
х* (х* ₁,х*₂ ), то такая функция называется мономодальной. Взаимное расположение ее линий уровня имеет  вид, изображенный на рис.2. 

Мультимодальными называются функции,  которые имеют  более одного экстремума. Такова, например, функция Химмельблау  
F(x) = (x₁²+x₂-11)²+(x₁+x₂²-7)², 
имеющая четыре изолированные точки минимума. На рис.3 схематично изображены линии уровня этой функции.  

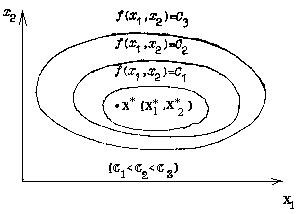
Рис.2

Чтобы найти точку х* локального минимума функции f(х),  составляют последовательность точек (приближений к решению)  {х^(k)} (k=0,1, ...) , сходящуюся к точке  х*  
(k=0,1,...), сходящуюся к точке х*.

Последовательность значений функции f(х^(k)) должна быть  монотонно убывающей и ограниченной снизу:
f(x⁽⁰⁾) > =f(x⁽¹⁾) > = . . . > =f(x^(k)) > = . . . > =f(x⁽*⁾).
Геометрический образ решения задачи (2)  для случая  двух переменных напоминает спуск на дно чаши. Это мотивирует названия методов решения задачи (2) -  «методы спуска».
Для различных методов спуска сначала выбирают начальную точку последовательности х⁽⁰⁾. Дальнейшие приближения  х(k) определяются соотношениями

x^(k+1)=x^(k)+t^(k)S^(k) (k= 0, 1, 2, . . .), (12)
Где S^(k) - вектор направления спуска; скалярная величина t^(k) я|вляется решением задачи одномерной минимизации

f(x^(k)+ts^(k))-->min,   tОR.  (13)

Таким образом, задача поиска минимума функции нескольких переменных сводится к последовательности задач одномерной минимизации (13) по переменной t на отрезках n-мерного пространства, проходящих через точки х^(k)  в направлении векторов S^(k).
Методы спуска различаются выбором вектора спуска и способом  юшения задачи одномерной минимизации.
При решении последовательности задач (12) можно ограничиться методом сканирования для поиска минимума функции одной переменюй. Выбрав произвольно начальную точку х⁽⁰⁾ и размер начальюго шага h по переменной t, в методе сканирования можно   получить различные точки минимума мультимодальной функции.
Если функция f(x) мономодальна, то независимо от выбора начальной точки траектория поиска должна привести к единственной точке локального минимума этой функции.

Подавляющее число реальных задач оптимизации, представляющих практический интерес, являются многомерными: в них целевая функция зависит от нескольких аргументов, причем иногда их число может быть весьма большим.

Вспомним, например, задачу о химическом производстве. Мы отметили, что в ней целевая функция зависит от температуры, и при определенном ее выборе производительность (выход интересующего нас продукта) оказывается максимальной. Однако, наряду с температурой, производительность зависит также от давления, соотношения между концентрациями вводимого сырья, катализаторов и ряда других факторов. Таким образом, задача выбора наилучших условий химического производства - это типичная многомерная задача оптимизации. Математическая постановка "таких задач аналогична их постановке в одномерном случае: ищется наименьшее (наибольшее) значение целевой функции, заданной на некотором множестве Е возможных значений ее аргументов. В случае, когда целевля функция непрерывна, а множество Е является замкнутой ограниченной областью, остается справедливой теорема Вейерштрасса. Тем самым выделяется класс задач оптимизации, для которых гарантировано существование решения. В дальнейшем мы всегда будем предполагать, не оговаривая этого особо, что все рассматриваемые задачи принадлежат этому классу. Как и в одномерном случае, характер задачи и соответственно возможные методы решения существенно зависят от той информации о целевой функции, которая нам доступна в процессе ее исследования. В одних случаях целевая функция задается аналитической формулой, являясь при этом дифференцируемой функцией. Тогда можно вычислить ее частные производные, получить явное выражение для градиента, определяющего в определяющего в каждой точке,направления возрастания и убывания функции,

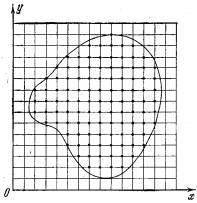
Рис. 1.

Построение сетки с шагом h и выбор "пробных" точек в узлах сетки для приближенного определения наименьшего значения функции двух переменных. и использовать эту информацию для решения задачи. В других случаях никакой формулы для целевой функции нет, а имеется лишь возможность определить ее значение в любой точке рассматриваемой области (с помощью расчетов, в результате эксперимента и т. д.). В таких задачах в процессе решения мы фактически можем найти значения целевой функции лишь в конечном числе точек, и по этой информации требуется приближенно установить ее наименьшее значение для всей области. Многомерные задачи, естественно, являются более сложными и трудоемкими, чем одномерные, причем обычно трудности при их решении возрастают при увеличении размерности. Для того чтобы вы лучше почувствовали это, возьмем самый простой по своей идее приближенный метод поиска наименьшего значения функции, который уже обсуждался для одномерных задач в . Покроем рассматриваемую область сеткой с шагом  h (рис. 1) и определим значения функции в ее узлах. Сравнивая полученные числа между собой, найдем среди них наименьшее и примем его приближенно за наименьшее значение функции для всей области. Как мы уже говорили выше, данный метод используется для решения одномерных задач. Иногда он применяется также для решения двумерных, реже трехмерных задач. Однако для задач большей размерности он практически непригоден из-за слишком большого времени, необходимого для проведения расчетов. Действительно, предположим, что целевая функция зависит от пяти переменных, а область определения является пятимерным кубом, каждую сторону которого при построении сетки мы делим на 40 частей. Тогда общее число узлов сетки будет равно 41⁵~10⁸. Пусть вычисление значения функции в одной точке требует 1000 арифметических операций (это немного для функции пяти переменных). В таком случае, общее число операций составит 10¹¹. Если в нашем распоряжении имеется ЭВМ с быстродействием 1 млн. операций в секунду, то для решения задачи с помощью данного метода потребуется 10⁵ секунд, что превышает сутки непрерывной работы. Добавление еще одной независимой переменной увеличит это время в 40 раз. Проведенная оценка показывает, что для больших задач оптимизации метод сплошного перебора непригоден. Иногда сплошной перебор заменяют случайным поиском. В этом случае точки сетки просматриваются не подряд, а в случайном порядке. В результате поиск наименьшего значения целевой функции существенно ускоряется, но теряет свою надежность.

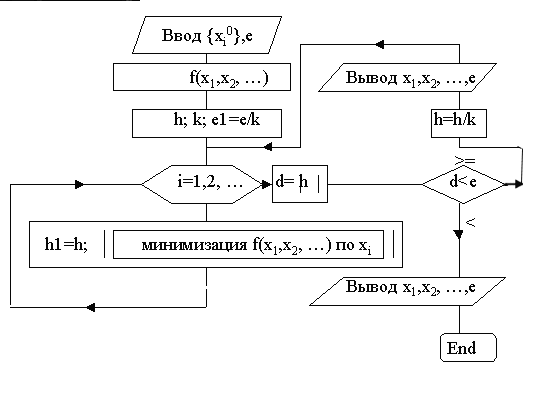
Метод покоординатного спуска.

Пусть нужно найти наименьшее значение целевой функции u=f(M)=f(x₁, x₂, . . . ,x_n). Здесь через М обозначена точка n-мерного пространства с координатами x₁, x₂, . . . ,x_n: M=(x₁, x₂, . . . ,x_n). Выберем какую-нибудь начальную точку М₀=(x₁⁰, x₂⁰, . . . ,x_n⁰) и рассмотрим функцию f при фиксированных значениях всех переменных, кроме первой: f(x₁, x₂⁰,x₃⁰, . . . ,x_n⁰ ). Тогда она превратится в функцию одной переменной  x₁ . Изменяя эту переменную, будем двигаться от начальной точки x₁=x₁⁰  в сторону убывания функции, пока не дойдем до ее минимума при x₁=x₁¹, после которого она начинает возрастать. Точку с координатами ( x₁¹, x₂⁰,x₃⁰, . . . ,x_n⁰) обозначим через М₁, при этом f(M₀) >= f(M₁). Фиксируем теперь переменные: x₁=x₁¹, x₃= x₃⁰, . . . ,x_n=x_n⁰ и рассмотрим функцию f как функцию одной переменной  x₂: f(x₁¹, x₂², x₃⁰ . . . ,x_n⁰). Изменяя  x₂ , будем опять двигаться от начального значения x₂=x₂⁰   в сторону убывания функции, пока не дойдем до минимума при x₂=x₂¹ .Точку с координатами {x₁¹, x₂¹, x₃⁰ . . . x_n⁰} обозначим через М₂, при этом   f(M₁) >=f(M₂).

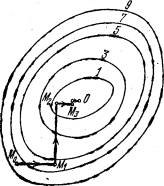
Рис. 2. Поиск наименьшего значения функции методом покоординатного спуска.

Проведем такую же минимизацию целевой функции по переменным   x₃, x₄,  . . . ,x_n. Дойдя до переменной x_n, снова вернемся к x₁ и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек М₀,М₁,М₂, . . . , которой соответствует монотонная последовательность значений функции f(M₀) >= f (M₁)>= f(M₂) >=  ...    Обрывая ее на некотором шаге k можно приближенно принять  значение функции f(M_k) за ее наименьшее значение в рассматриваемой области.  Отметим, что данный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Если целевая функция   f(x₁, x₂, ... ,x_n)  задана явной формулой и является дифференцируемой, то мы можем вычисллить ее частные производные и использовать их для определения направления убывания функциипо каждой переменной и поиска соответствующих одномерных минимумов. В противном случае, когда явной формулы для целевой функции нет, одномерные задачи следует решать с помощью одномерных методов. На рис. 2 изображены линии уровня некоторой функции двух переменных             u= f (х, у). Вдоль этих линий функция сохраняет постоянные значения, равные 1, 3, 5, 7, 9. Показана траектория поиска ее наименьшего значения, которое достигается в точке О, с помощью метода покоординатного спуска. При этом нужно ясно понимать, что рисунок служит только для иллюстрации метода. Когда мы приступаем к решению реальной задачи оптимизации, такого рисунка, содержащего в себе готовый ответ, у нас, конечно, нет.  Пусть требуется решить задачу (2):

f(x) -->min, х ОRⁿ. (2)

В двумерном пространтсве R². Решение задачи (2) методом покоординатного спуска, иначе называемого методом Гаусса - Зейделя, производят по следующей общей схеме.
Выбирают произвольно начальную точку х⁽⁰⁾  из области определения функции f(х). Приближения х^(k) определяются соотношениями (3):
x^(k+1)=x^(k)+t^(k)S^(k) (k=0,1,2, ...),
где вектор направления спуска s^(k)- это единичный вектор, совпадающий с каким-либо координатным направлением (например, если S^(k) параллелен х₁, то S^(k)= {1,0,0,...,0}, если он параллелен x₂, то S^(k)={0, 1, 0, . . . ,0} и т.д.) ; величина t^(k)  является решением задачи одномерной минимизации:
f(x^(k)+ts^(k)) --> min, t ОR¹, (k=0,1,2, ...),
и может определяться, в частности, методом сканирования.
Детальная реализация общей схемы в двумерном случае R² дает траекторий приближения к точке х* методом покоординатного спуска, состоящую из звеньев ломаной, соединяющих точки х^(k), х~^(k), x^(k+1) (k=0, 1, 2,) (рис.2). При k=0, исходя из начальной точки х⁽⁰⁾=(x₁⁽⁰⁾,x₂⁽⁰⁾), находят точку х~⁽⁰⁾= (x₁~⁽⁰⁾,x₂⁽⁰⁾), минимума функции одной переменной f(x₁,x₂⁽⁰⁾); при этом f(x~⁽⁰⁾)<=f(x⁽⁰⁾).Затем находят точку минимума x⁽¹⁾  функции f (x₁~⁽⁰⁾,x₂) по второй координате. Далее делают следующий шаг вычислений при k=1. Полагают, что исходной точкой расчета является х⁽¹⁾. Фиксируя вторую  координату точки х⁽¹⁾, находят точку минимума х~⁽¹⁾= (x₁~⁽¹⁾,x₂⁽¹⁾), функции f(x₁,x₂⁽¹⁾) одной переменной x⁽¹⁾; при этом f(x~⁽¹⁾)<=f(x⁽¹⁾)<=f(x⁽⁰⁾). Точку х⁽²⁾ получают, минимизируя целевую функцию f(x₁~⁽¹⁾,x₂), вновь по коорданате х₂, фиксируя координату x₁~⁽¹⁾ ,точки x⁽¹⁾ , и т.д.
Условием прекращения вычислительной процедуры при достижении заданной точности e может служить неравенство
||x^(k+1) - x^(k) ||<e (4)

Блок-схема поиска минимума функции двух переменных методом покоординатного спуска.

Метод градиентного спуска.

Рассмотрим функцию f, считая для определенности, что она зависит от трех переменных x,y,z. Вычислим ее частные производные дf/дх, дf/ду, дf/дz и образуем с их помощью вектор, который называют градиентом функции:

grad f(x, у, z) = дf (х, у,z) /дх*i+дf( x, у, z)/ду*j+дf(x, y,z)/дг*k.

Здесь i, j, k - единичные векторы, параллельные координатным осям. Частные производные характеризуют изменение функции f по каждой независимой переменной в отдельности. Образованный с их помощью вектор градиента дает общее представление о поведении функции в окрестности точки (х, у,z). Направление этого вектора является направлением наиболее быстрого возрастания функции в данной точке. Противоположное ему направление, которое часто называют антиградиентным, представляет собой направление наиболее быстрого убывания функции. Модуль градиента

(|grad(х, у,z)|)²=(дf/дх (х, у,z))² +(дf/ду( x, у, z))²+(дf/дг(x, y,z))²

определяет скорость возрастания и убывания функции в направлении градиента и антиградиента. Для всех остальных направлений скорость изменения функции в точке (х, у, z) меньше модуля градиента. При переходе от одной точки к другой как направление градиента, так и его модуль, вообще говоря, меняются. Понятие градиента естественным образом переносится на функции любого числа переменных. Перейдем к описанию метода градиентного спуска. Основная его идея состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея реализуется следующим образом. Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции. Специальный выбор направления движения на каждом шаге позволяет надеяться на то, что в данном случае приближение к наименьшему значению функции будет более быстрым, чем в методе покоординатного спуска. Метод градиентного спуска требует вычисления градиента целевой функции на каждом шаге. Если она задана аналитически, то это, как правило, не проблема: для частных производных, определяющих градиент, можно получить явные формулы. В противном случае частные производные в нужных точках приходится вычислять приближенно, заменяя их соответствующими разностными отношениями:

дх ~ (дf ~  f(x₁, ...,x_i+Dx_i, ..., x_n) - f(x₁, ..., x_i, ..., x_n))/Dx_i

Отметим, что при таких расчетах Dx_i ,нельзя брать слишком малым, а значения функции нужно вычислять с достаточно высокой степенью точности, иначе при вычислении разности  Df(x₁, ...,x_i+Dx_i, ..., x_n) - f(x₁, ..., x_i, ..., x_n) будет допущена большая ошибка.  На рис. 3 изображены линии уровня той же функции двух переменных u= f (х, у), что и на рис. 2, и приведена траектория поиска ее минимума с помощью метода градиентного спуска.

Сравнение рис. 2 и 3 показывает, насколько более эффективным является метод градиентного спуска.

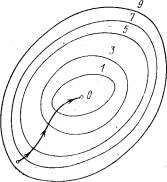
Рис. 3. Поиск наименьшего значения функции методом градиентного спуска

Метод наискорейшего градиентного спуска.

Вычисление градиента на каждом шаге, позволяющее все время двигаться в направлении наиболее быстрого убывания целевой функции, может в то же время замедлить вычислительный процесс. Дело в том, что подсчет градиента - обычно гораздо более сложная операция, чем подсчет самой функции. Поэтому часто пользуются модификацией градиентного метода, получившей название метода наискорейшего спуска.  

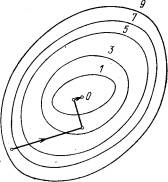
Рис.4 Поиск наименьшего значения функции методом наискорейшего спуска

Согласно этому методу после вычисления в начальной точке градиента функции делают в направлении антиградиента не маленький шаг, а движутся до тех пор, пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют описанную процедуру. При этом градиент вычисляется гораздо реже, только при смене направлений движения.

На рис. 4 показана траектория поиска наименьшего значения целевой функции по методу наискорейшего спуска. . Функция выбрана та же, что и на рис.2, 3. Хотя траектория ведет к цели не так быстро, как на рис. 3, экономия машинного времени за счет более редкого вычисления градиента может быть весьма существенной.

/источник информации: http://school-sector.relarn.ru/dckt/projects/optim/index.htm

Пример:

скачать файл MathCad (для оптимизации другой функции нужно поменять только формулу f(x1,x2):=(x1+1)⁴+(x2+1)⁴+(x1+1)²+(x2+1)² на ту которая Вам нужна; ответ смотрите в конце документа.)